• Craps Probability Distribution
• Blackjack Probability Distribution

Description

A Monte Carlo simulation of the dice game 'craps'.Returns a point estimate of the probability of winning craps using fair dice.

Usage

• The odds of rolling no 3's 50 times in a row is just that probability raised to the 50th power. It works out to around 57 times per 1000 games (here, the syntax 2^20 means 2 raised to the 20th power). (1-2/36)^50=0.057 Conceptually, the 3 and the 11 go together, since they occur with the same odds.
• Note: The above outcome over 36 rolls occurs only with a perfect distribution, which is unlikely, but useful for illustrating how and why odds are important in the game of craps. We know there are six ways to roll a 7 and three ways to roll a 10.

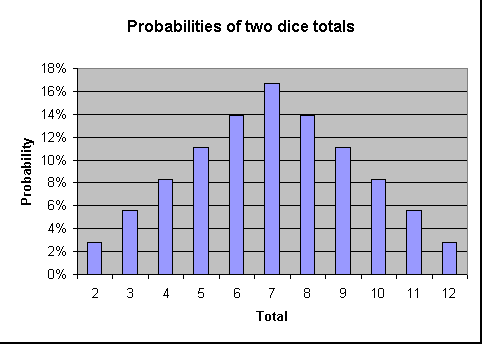
This video we create he probability distribution table for the sum of two dice.

Arguments

nrep	number of replications (plays of a single game of craps)
seed	initial seed to the random number generator (NA uses current state of random number generator; NULL seeds using system clock)
showProgress	if TRUE, displays a progress bar on screen during execution

Details

Implements a Monte Carlo simulation of the dice game craps played with fairdice.A single play of the game proceeds as follows:

• Two fair dice are rolled. If the sum is 7 or 11, the player winsimmediately; if the sum is 2, 3, or 12, the player loses immediately.Otherwise the sum becomes the point.

• The two dice continue to be rolled until either a sum of 7 is rolled(in which case the player loses) or a sum equal to the point isrolled (in which case the player wins).

The simulation involves nrep replications of the game.

Note: When the value of nrep is large, the function will executenoticeably faster when showProgress is set to FALSE.

Value

Point estimate of the probability of winning at craps (a real-valued scalar).

Author(s)

Barry Lawson (blawson@richmond.edu),Larry Leemis (leemis@math.wm.edu)

Examples

There are 6^2 = 36 possible outcomes when we re-roll the 1 and the 4. We first calculate the number of different outcomes that result in a particular hand and use this to determine the probability of each hand. For example, the probability of rolling a 2 and a 6 is 2/36 since we could roll the 2 and then the 6, or the 6 and then the 2. The probabilities of each of the hands are:

Hand	Number of Outcomes	Probability	Straight
6 - 2	2	2/36 = 1/18	Large
1 - 2	2	2/36 = 1/18	Large
6 - (not 2)	4 · 2 + 1 = 9	9/36 = 1/4	Small
2 - (not 1 or 6)	3 · 2 + 1 = 7	7/36	Small
no 2 or 6	4^2 = 16	16/36 = 4/9	None

Craps Probability Distribution

Note that a six paired with any other number can occur two ways, but a pair of sixes occurs in only one way. This is why the third and fourth rows have a plus one in the number of outcomes column.

Next, for each of the possible first roll outcomes we calculate the probability of getting a large straight or a small straight on the third roll. For the 6-2 and 1-2 hands we already have our large straight so we are done. For the 6 - (not 2) hand we re-roll the non-2 die. We have a 1/6 chance of getting a two and a large straight, and a 5/6 chance of not getting a 2 and having only a small straight. For the 2 - (not 1 or 6 hand) we will keep the 2,3,4,5 and re-roll one die, giving us a 1/3 chance at rolling a large straight and a 2/3 chance of having only a small straight. In the case where we rolled no 2 or 6 on the second roll, the situation for our third roll is the same as the situation for our second roll, so the above table gives the probabilities of each outcome.

Combining these results we see that the probability of a large straight is

1/18 + 1/18 + (1/4) · (1/6) + (7/36) · (1/3) + (4/9) · (1/18 + 1/18) &asymp 0.267.

The probability of a small straight (but not a large straight) is

(1/4) · (5/6) + (7/36) · (2/3) + (4/9) · (1/4 + 7/36) &asymp 0.535.

The probability of getting no straight at all is (4/9)² &asymp 0.198.

If we re-roll only one die, then on our second roll we have a 1/6 chance of rolling a 2 and getting a large straight. We also have a 1/6 chance of getting a 6 and a small straight. In this case, on our third roll we have a 1/6 chance of rolling a 2 and getting a large straight. However, 2/3 of the time we get neither a 2 or a 6 on our first roll in which case our situation does not change. Therefore our chance of getting a large straight is

Blackjack Probability Distribution

1/6 + (1/6) · (1/6) + (2/3) · (1/6) &asymp 0.306

The probability of getting only a small straight is

(1/6) · (5/6) + (2/3) · (1/6) = 0.25.

The chance of getting no straight is (2/3)² = 4/9 &asymp 0.444. So re-rolling only the 4 gives you a slightly higher chance of getting the large straight, but a much lower probability of at least ending up with a small straight. If you only need a large straight then re-rolling just the four is the better strategy, but if a small straight would also be valuable then re-rolling the 1 and the 4 might be a better move.